Attention in Neural Networks from Scratch

Attention is everywhere in AI these days… on it, in it, all around it. But what exactly is it? How does it work? And more importantly, why does it work?

Most explanations jump straight into embeddings, self-attention, transformers… it can be a lot. If you’re new or a bit rusty, it’s like getting a recipe in another language, leaving you lost in translation with just vibes and a confusing list of ingredients.

This post aims to change that, or at the very least, hand you a pot and show you where the stove is.

Here’s what’s on the menu:

We’ll start from scratch, building up step by step — from linear models to classic neural networks to polynomial functions.
We’ll keep things intuitive, using a single, cooking-themed example — with friendly explanations, minimal math, and plenty of interactive visuals.
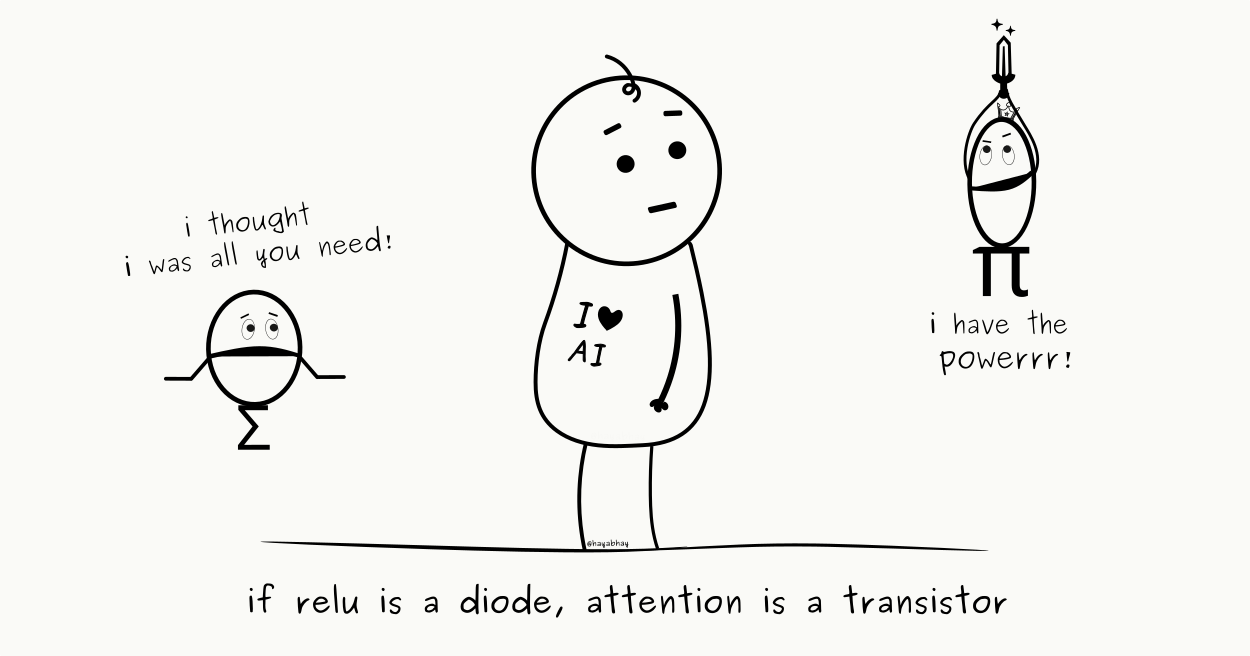
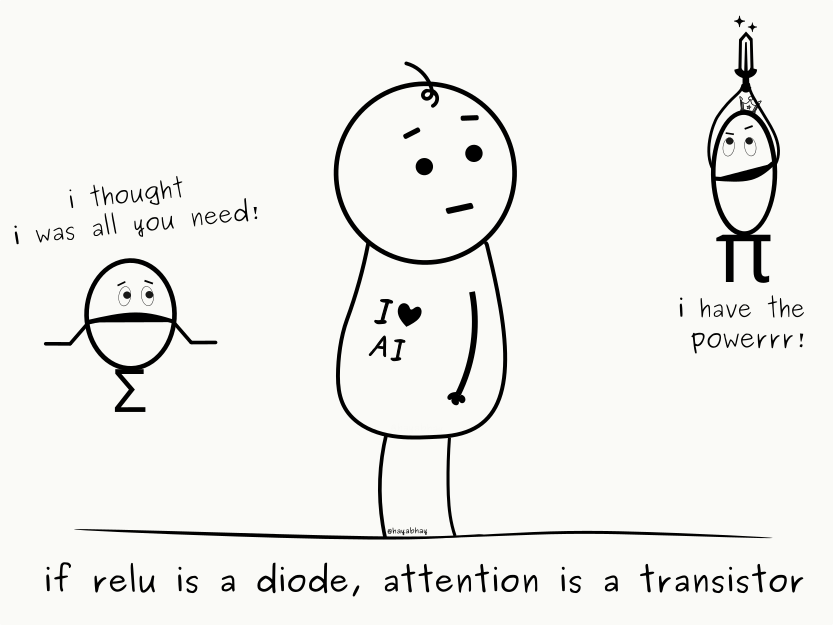
We’ll explore a handy metaphor, thinking of attention as a transistor — a flexible, higher-order switch compared to the simpler, diode-like ReLU.
And most importantly, we’ll take our time, simmering through the details and treating this like a slow-cooked meal — not a microwave dinner!

Whether you’re new to AI or just need a refresher, I hope this post deepens your understanding, sparks a chuckle, and most of all, keeps your undivided attention :)

1. let’s cook… rice!

As is tradition with machine learning explainers, let’s start with the simplest concept of them all — linear regression.

To set the stage, imagine you just bought a fancy new rice cooker and you’re ready to take that first step toward independence — learning how to cook. But before you can enjoy a perfect bowl of rice, you need to answer one key question — how much water to add to cook it just right?

Sure, you could read the instructions, but you’re the type who refuses to ask for directions when lost. So instead, you start experimenting — testing different water-to-rice ratios and carefully noting what works best. After a few attempts, you’ve gathered a small set of data points — your very own rice-cooking wisdom!

And just like that, you’ve stumbled into a classic regression problem. I won’t bore you with the nitty-gritty of gradient descent, but take a look at the figure below. You’ll see a simple pattern emerge — for every 1 cup of rice, you need about 2 cups of water.

In math speak, this can be expressed as:

\text{cups of water} = 2 \times \text{cups of rice}

Or more generally:

y = 2x

which fits the standard linear equation format:

y = ax + b

where $a$ is the coefficient (or slope, or weight) — $2$ ; and $b$ is the intercept (or bias) — $0$ .

And this equation, $y = 2x$ , is now your model — your go-to expert — for serving up perfect rice, every single time.

refresher: linear regression.

If this doesn’t feel familiar, think of it like playing connect the dots with the data points you’ve collected. You could draw a squiggle, a zigzag, or even a loop. But the simplest option is a straight line.

In Machine Learning (ML), we don’t just eyeball where this line should go — we use a systematic approach, an algorithm, to find the best-fitting line.

The most common one, gradient descent, starts with a random line — a linear equation like $y = ax + b$ , with $a$ and $b$ as random values. Then, it repeatedly does the following:

First, it measures how well the current line fits the data using a loss function.

A loss function quantifies the gap between expectation and reality — what the line predicts versus what we actually observe — and expresses it as an error term to minimize. In our case, we’ll use mean squared error — a fancy way of saying, “square all the differences and take the average.”
Next, it adjusts the line by tweaking $a$ and $b$ to reduce that error.

Again, it doesn’t just yolo it — it uses calculus to calculate the gradient of the loss function. That gradient tells it whether to increase or decrease $a$ and $b$ , and by how much. That’s why it’s called gradient descent — the algorithm “descends” down the loss function to find the lowest possible error.

With each iteration, the algorithm fine-tunes the line, reducing the gap between predictions and actual data. The end result is a trained line with the best values for $a$ and $b$ — commonly known as the model.

Why call it a model? Because it approximates the relationship between the input (cups of rice) and the output (cups of water).

And this model behaves like an expert, capable of predicting how much water is needed for any amount of rice… just like a seasoned cook!

what is linear really?

The term linear is often used to mean a straight line, but there’s a bit more to it.

Intuitively, a linear transformation is one that preserves straightness and proportionality. That’s just a fancy way of saying straight lines stay straight, and evenly spaced points stay evenly spaced — only stretched or squished.

But more formally, only an equation like $y=ax$ is linear because it also preserves the origin — meaning $f(0) = 0$ . If you add a constant ( $y = ax + b$ ), the line shifts away from the origin, making it an affine transformation.

That said, in machine learning, linear is often used loosely to refer to both linear and affine transformations.

2. new rice, who dis?

Feeling like a master chef, you bring your finest bowl of rice to your neighbor for a taste test. They take a bite, nod like they’re impressed, and toss you a mysterious bag.

“Okay chef… but can you handle this?”

You peek inside. It looks like rice — sort of — but the grains are dark, chonky, and just… different.

“Easy peasy,” you shrug. “How hard can it be?”

You head back to your kitchen and stick to your trusty formula — one cup of rice, two cups of water — and let the cooker do its thing.

After a short wait — beeeep. Done. Your moment of truth has arrived.

You pop the lid, take a bite, and… uh-oh.

Chewy. Tough. Definitely undercooked. Somewhere in the back of your mind, you can almost hear your neighbor chuckling: “Told you so.”

Turns out, your model wasn’t so general after all. It worked great for cooking one type of rice — but this new variety? Not so much.

So, what now? It’s back to experimenting — cooking, taking notes, fitting lines. And before long, you’ve got a new set of data points and a new pattern. Looks like this rice is thirsty — it needs 3 cups of water per cup of rice to cook just right.

In math speak, you now have a new equation — still linear, but with a different slope:

y = 3x

And this equation is your new model — your go-to expert — for cooking this new kind of rice to perfection.

3. a ricey dilemma.

So far, we’ve cooked up not one, but two models — each perfectly tuned to a different type of rice, thanks to data and good ol’ gradient descent.

That’s great… but also kind of a headache. Now we’re stuck juggling them like we’re in a rice-themed circus. And hey! We’re going for a cooking show here, not a clown show… not yet.

And that brings us to the real challenge — how do we merge these two models into a single one that works for any type of rice?

If we were naive, we’d treat all rice the same and fit a single line. That would land us at around 2.5 cups of water per cup of rice — a recipe for disappointment that always overcooks white rice and undercooks the other.

But we’re not naive — and we don’t really cook like that either. When we’re in the kitchen, we simply pick the right model depending on the rice we’re cooking.

So our next move? Write a rule that does exactly that — a simple if-else to switch between the two models:

if rice is white
    cups_of_water = 2 x cups_of_rice (y = 2*x)
else
    cups_of_water = 3 x cups_of_rice (y = 3*x)

Great..! We’ve solved our dicey-ricey dilemma but now we’ve got a new problem. Our solution is part machine-learned (the two models) and part human-coded (the if-else rule).

In an ideal world, the model wouldn’t need our help — it would learn when to switch all on its own, purely from data. No if-else required.

In an ideal world… we’d have one model to rule them all.

4. one model to rule them all.

At this point, you’re either craving a burrito, questioning my sanity, or most likely, both. But you’ve stuck with me like sticky rice, and for that, I salute you. Now, I promise… we’re about to get to the good stuff!

To ditch our hardcoded if-else switch, let’s step back and ask ourselves: how do we make this decision?

We don’t just pick randomly — we observe. We notice that the second type of rice is darker, and that’s our cue to switch equations.

But our model? It’s flying blind. It has no idea what type of rice it’s dealing with, so it can’t make the same decision we do. If we want it to learn when to switch — just like we do — we first need to give it a way to see what we see.

With this realization, you go full mad scientist. You scrap everything, buy a luminance meter — a fancy gadget that measures light — and start collecting a fresh set of data points. But this time, you don’t just track cups of rice and water; you also record how dark the rice appears.

This new variable — let’s call it $z$ — ranges from $0$ (white) to $1$ (black). And with that, a whole new world opens up — a 3D world!

Take a look at the plot below — zoom in, rotate, and explore. The patterns practically jump out at us. But to our model, they’re just a bunch of numbers. It still has to learn what we can understand at a glance.

Now, our quest begins.

Our first shot at this “one model to rule them all” starts with the same trick as before — linear regression. But with an extra variable, we’re no longer fitting a line — we’re fitting a plane!

In math terms, we’re now solving for:

y = ax + bz + c

where:

$a$ determines the water needed per cup of rice,
$b$ adjusts for the type of rice, and
$c$ represents the baseline amount of water.

In simpler terms, we’re setting a fixed water-to-rice ratio, and then adding or removing a fixed amount of water depending on how dark the rice is.

To really drive this home, let’s plug in some numbers:

Suppose $a = 2$ , $b = 1$ , and $c = 0$
For white rice ( $z \approx 0$ ), the equation simplifies to $y \approx 2x$ — exactly what we want.
But for the darker variety ( $z \approx 0.5$ ), the equation becomes $y \approx 2x + 0.5$ — not the $y = 3x$ we need.

In fact, no matter how you tweak these numbers, this model actually always undercooks or overcooks one type of rice at certain amounts. The 3D plot below makes this clear — our best-fitting plane from gradient descent simply can’t fit all our data points.

Why? Because the relationship isn’t linear.

Rice be like, “I’m a multi-layered masterpiece — not instant noodles.” And honestly? Facts.

5. flexing ‘em curves.

By now, you’re probably thinking, “Alright, if a flat plane won’t cut it, why not go curvier?” And you’d be absolutely right! Instead of forcing a rigid plane where it doesn’t fit, we need something more flexible — something that bends the knee to our rice overlords.

Enter neural network and its favorite joint: ReLU.

ReLU (short for Rectified Linear Unit) is an activation function that gives neural networks the non-linear flex they need to learn complex functions. It’s simple: it leaves positive values as-is while crushing negatives to zero.

Now why ‘o why does this matter?

On its own, a linear function can move, stretch, or rotate a line but no matter what, it stays straight. Adding a ReLU changes that. It introduces a kink — a sharp corner — so the model can flex the line instead of keeping it straight. The more ReLUs you have, the more corners you can introduce. For example, with three ReLUs, you can introduce up to three corners to your line.

three-reLUs — a ReLU layer adding kinks to a line.

This lets you build jagged, step-like functions and, with enough ReLUs, you start approximating curves as a bunch of tiny line segments. A very kinky function!

This is called piecewise linearity — a fancy way of saying “a curve made from many tiny lines.” And since neural networks stack tons of these, they become universal approximators, capable of modeling pretty much any function.

piecewise linearity visualized.

To get a better feel for how ReLUs approximate curves, let’s walk through a few examples.

We’ll start with a simple one: $y = x^2 + 1$ .

This is a quadratic — a second-order polynomial of the form $y = ax^2 + bx + c$ . It’s got a smooth curve and a single turning point.

Next up: $y = x^3 - 2x^2 + 1$ .

This one’s cubic — a third-order polynomial of the form $y = ax^3 + bx^2 + cx + d$ . Its shape is more complex, with two turning points.

Finally, let’s wrap things up with a classic: $y = \sin(2x)$ .

In higher dimensions, the same principle applies. Instead of line segments, you have planes and hyperplanes that come together to form complex surfaces.

That’s the power of piecewise linearity — stack enough pieces in the right places, and you get complexity from simplicity… one piece at a time!

activate: more activations.

While ReLU is the usual go-to, it’s far from the only activation function. Plenty of others exist, each with its own quirks — some subtle, some dramatic.

At their core, though, they all serve the same purpose: shaping how information flows through a neural network.

Let’s take a quick look at some classics.

First up, the binary activation function — the simplest of the lot.

It applies a hard threshold, usually at $0$ : if the input is positive, the output is $1$ ; otherwise, it’s $0$ .

Think of it as a basic detector — either on or off, nothing in between. Like a fuel light that stays off when you have enough gas, but flips on when it falls below a certain level.
Next, we’ve got the smooth operators — sigmoid and tanh.

Unlike binary activation, these don’t jump between values — they ease into them.

Sigmoid compresses everything into a range between $0$ and $1$ , while tanh stretches that range from $-1$ to $+1$ . In fact, tanh is just a scaled and shifted version of sigmoid, centered around $0$ instead of $0.5$ .

You can think of these like dimmer switches — they still control the flow, but do it gradually rather than simply turning on or off.
And lastly, we return to our familiar friend — ReLU.

Like the binary activation function, it has a hard threshold (at $0$ ) — but instead of snapping to $1$ , it passes positive values straight through.

You can think of it like a gate — shut tight for anything negative, then swinging wide open the moment something positive comes knocking.

It’s almost like it’s saying, “Positive vibes only.”

Here’s what they look like for comparison:

As you can see, both sigmoid and tanh are smooth, S-shaped curves that taper off at the edges. But if you look a little closer, there’s something even more interesting — near the center of their range, they behave almost linearly. This helps them preserve the signal’s structure through the middle while gently flattening out the extremes.

And like ReLU, when stacked across multiple units, they can also shape the output in complex ways — just with a softer touch. Here’s that same 3-ReLU plot again, now with sigmoid and tanh activations for comparison:

Now that we’ve got the idea, let’s try it out.

We’ll start simple — one hidden layer, a few ReLUs — and let gradient descent do its thing.

What you now get is a flexible model that bends to fit our data points, bringing us one step closer to that one model to rule them all.

The plot below shows this in action, comparing models with two and ten ReLU units in a single hidden layer — along with a few test points to see how well they handle unseen data.

what I mean when I say ReLU.

Formally, ReLU refers to the function $f(x) = \max(0, x)$ .

What does that actually mean? The Rectified part just means negative values get set — or “rectified” — to zero. The Linear part means that for positive values it behaves like the simple identity function: $f(x) = x$ .

In a neural network, each computational unit (or neuron) typically has two parts — a linear function, followed by an activation function. Technically, “ReLU” refers only to the activation function, but in practice, it’s common, if a bit loose, to use “ReLU” as shorthand for the entire unit — a ReLU-activated unit.

Throughout this post, I’ll use “ReLU” in this broader, more casual sense to refer to the full unit to keep things simple. But when needed, I’ll make it clear if I’m referring specifically to the activation function itself.

As you can see, with just two units, the model improves over a plane — even if a little jagged. With ten units, it starts to smooth out, and hug the data even tighter.

But if you look closer, you can see that while the fit looks great for the data we’ve collected, it starts to stumble beyond it. For instance, if you decide to cook, say, 10 cups of rice, you might just end up with a soggy mess… or a crunchy surprise.

Darn it! The quest continues.

6. a higher order.

Back in your kitchen, things are a little less complicated.

Having tamed the mystery rice your neighbor gave you, you bring over a freshly cooked bowl for another taste test. Once again, they take a bite and nod like they’re impressed.

“What kind of rice was that, anyway?” you ask.

“Oh, that’s just regular rice. It just has a lot of bran.”

“Bran?” you ask, confused.

“Yeah, the outer layer of the rice. They usually remove it to make white rice. Here, take this,” they say, handing you a bag. “This one’s got a little bran left.”

You walk back home, deep in thought. Bran, huh? Today I learned.

By now, your obsession with building a single model to cook rice has completely eclipsed your original obsession with simply making great rice. And to make matters worse, a bunch of artificial neurons just outsmarted you — just like those dark rice grains did earlier.

And no… you will not let them do you like that!

So what secret did that sneaky neural network uncover that you couldn’t? Its time to take a step back and rethink.

Before all this neural network wizardry, we had two simple equations:

for white rice: $y=2x$
for the darker variety: $y=3x$

The only difference was the water-to-rice ratio — $2$ and $3$ — or in math speak, the slope. And the reason behind this? You just found out — the bran!

Our first attempt at a single model flopped because we treated rice’s darkness ( $z$ ) as just another variable in our original linear equation: $y=ax+bz+c$ .

In that setup, $z$ could only nudge the total amount of water up or down — like tossing in some extra water at the end and hoping for the best.

What it couldn’t do was something deeper — something more fundamental. It couldn’t change the rule itself — the amount of water needed per cup of rice!

And that is the key insight.

Our dark rice isn’t whispering, “Just throw in some extra water and yolo.” It’s straight-up shouting, “Change the whole rule, chef!”

In math speak, rice’s darkness ( $z$ ) isn’t just nudging the output — it’s actually changing the slope ( $a$ ). So those numbers in our equations — $2$ and $3$ — aren’t magical constants gifted by gradient descent anymore. They’re directly related to how much bran the rice has — how dark it appears.

And what’s the exact relationship? We don’t know yet. And when in doubt, we keep it simple — we start with a linear one.

So instead of treating $a$ as a fixed constant, we can let it flex with $z$ using a new linear equation:

a = pz + q

Merging this with our original equation, we get:

\begin{aligned} y &= (pz + q)x + b \quad \text{or,} \\[1em] y &= pxz + qx + b \end{aligned}

And just like that, we’ve arrived at a higher-order model — a polynomial.

So how does it fit? Like a glove — not just for unseen test points, but even for that new bag of rice that had a little bran on it.

Why? Let’s plug in some numbers like we did before:

Suppose $p = 2$ , $q = 2$ , and $b = 0$ , our equation becomes: $y = 2xz + 2x$
For white rice ( $z \approx 0$ ), this further simplifies to $y \approx 2x$ — exactly what we want.
For the darker variety ( $z \approx 0.5$ ), the equation now becomes $y = 3x$ — bingo!

Of course, we can use gradient descent to learn these parameters from our data — and sure enough, it finds the perfect fit.

a note on the narrative.

The story here is meant to illustrate the core idea behind higher-order models in a way that’s intuitive and relatable. The linear assumption ties into the idea that more bran means darker rice — which, intuitively, tracks with needing more water.

I’ve deliberately skipped over testing rice with more levels of bran to keep the narrative focused. But it’s easy to imagine your neighbor showing up with another bag — this time with, say, half the bran… or most of the bran. And just as easy to imagine them all fitting neatly into our polynomial model.

Of course, the actual relationship of bran and its effect on water needs might be very different. I have no idea how bran actually works, and I’m not a rice scientist :)

So that’s what our neural network was up to — uncovering a hidden higher-order relationship, one ReLU at a time. With each added unit, it inched closer to mimicking the underlying polynomial curve, piecing together a kinky approximation.

But this comes at a cost. While each unit adds flexibility, it also introduces more parameters — values our network has to learn from data using gradient descent.

Why? Because each unit has two parts — a linear function and an activation. The activation doesn’t need parameters, but the linear part does: one weight per input, plus a bias.

And then there’s the output unit, which combines everything into a final prediction — adding one weight per hidden unit, plus its own bias.

Here’s a quick breakdown of this parameter cost for our three models:

the jagged 2-ReLU model needs 9 parameters: that’s 2 weights (for $x$ and $z$ ) $+$ 1 bias per unit $\times$ 2 hidden units $+$ 3 for the output — $(2+1) \times 2 + 3 = 9$ .
the smoother 10-ReLU version needs 41 parameters — 30 for the hidden and 11 for the output units.
but the polynomial model needs just 3 parameters: $p$ , $q$ , and $b$ .

Why? Despite their non-linear reputation, ReLUs are still piecewise linear. They can only approximate curves by stacking together. But polynomials? They curve on their own — no ReLU construction crew needed!

And with that, we’ve now arrived at a different kind of computational unit: the sigma-pi unit.

Linear units — even when ReLU activated — rely on additive interactions, combining inputs through weighted sums:

\sum_{i} w_i x_i

Sigma-pi units, on the other hand, introduce multiplicative interactions — capturing higher-order relationships directly through weighted products:

\sum_{i} w_i \prod_{j} x_j

That’s where the name comes from — sigma ( $\sum$ ) for addition and pi ( $\prod$ ) for multiplication. Stack these higher-order units together, and you’ve built yourself a higher-order network.

And it is this kind of higher-order relationship that lies at the heart of attention mechanisms in neural networks.

a note on sigma-pi units.

The formulation above is intentionally simplified to highlight the core idea. In practice, sigma-pi units come in many forms, capturing different levels of higher-order interaction. Some compute just pairwise products between inputs, while others model more complex combinations — depending on the task and network architecture.

Here, I’ve used “sigma-pi units” as a loose conceptual umbrella to introduce multiplicative interactions and the broader idea of higher-order networks.

And this concept isn’t new — it’s appeared in various forms across machine learning, even if not always labeled explicitly. A well-known example is the gating mechanism in recurrent networks like LSTMs and GRUs, which use multiplicative interactions between inputs and hidden states to control information flow.

Intermission: Take a deep breath. Stretch. Eat a Cheeto.

7. more grain, more pain.

So you did it. You cracked the code, uncovered the hidden relationship, and ascended to a higher order — all on your own, no neural network wizardry needed.

You’re basically the rice whisperer, the polynomial prophet, the grandmaster of grains. And, if there were a Mount Rice-more, your face would most definitely be on it.

But just as you’re about to bust out your victory dance — knock, knock.

Who’s there? Your neighbor. And they’re holding a bowl of… something.

“… is that rice?” you ask, squinting at the tiny, black grains that look nothing like rice.

“Not anymore… ” they say with a smile. “Been breeding this one for a while now. It’s got… stuff. A bit of this, a bit of that. Give it a try — you’ll like it.”

You take a deep breath, thank them for the gift, and head back to your kitchen.

Turns out, your neighbor isn’t just some rice snob — they’ve been on their own side quest. While you were cooking up rice models in your kitchen, they were cooking up genetic freaks in their backyard. And now, they’ve handed you their latest franken-grain, knowing damn well you’d drop everything to perfect it.

But this time, you’re sooo ready for this.

Still riding that polynomial high, you grab your freshly minted universal model and get to work. The grains are nearly black — which means a lot of bran, and a lot of water.

Your model agrees — 4 cups of water per cup of grain. Into the cooker it goes!

\begin{aligned} y &= 2xz + 2x\quad(z\approx1) \\[1em] y&\approx4x \end{aligned}

After a short wait — beeeep. Done. Your moment of truth has arrived… again.

You eagerly grab a spoon, lift the lid, and… mush. Not just any mush — soggy, sloppy, soupy mush.

Ughhh… not again!

Looks like this grain really is a genetic freak — and the model? A myopic flop.

So what now? You know the drill — small test batches, meticulous notes, new data, new pattern, new equation.

Turns out, this new grain only needs one cup of water per cup of grain — a simple:

y = x

Like before, all the equations differ only in their water-to-grain ratios — $2$ , $3$ , and $1$ . But this time, the neat little trick that made our polynomial model work — $a = pz + q$ — comes crashing down.

Why? Because last time, a grain’s appearance wasn’t just a random detail — it actually meant something. Darker grains had more bran, and more bran meant more water. That pattern held, the logic clicked, and our simple linear assumption worked just fine.

But this new grain just wrecked that logic… and you have no idea why!

Sure, if you had a fancy lab filled with high-tech gadgets, maybe you could analyze its molecular structure or decode its DNA to pinpoint every difference. But you’re not a molecular biologist. And more importantly, you don’t need to decode the universe — you just need a well-cooked bowl of grains.

So where does that leave us?

Our linear models, $y = ax + b$ , still hold — if we can set $a$ to the right water-to-grain ratio. And $a$ is still linked to $z$ — how dark the grain is — just not in a neat, linear way anymore.

But here’s the real silver lining in this grainy mess: we don’t actually need to know the exact relationship between $a$ and $z$ . In fact, we don’t even need to care.

Instead of trying to predict $a$ directly from $z$ in one clean swoop, we can use $z$ to first classify — or rather, pay attention to — the type of grain we’re dealing with and then switch to the right value of $a$ — the right model, the right expert.

So how do we do that? if-else statements? No way.

We’re going back to neural networks — but this time, from a state of higher-order enlightenment.

8. better switch.

So far, the grain train has been a wild ride.

Life was easy when relationships were linear — you could just rail straight through them. Even when things got bendy, you lucked out with a higher-order fit and went full polynomial.

But you’re off the rails now. Franken-grain has taken over the engine room, and stranger grains may not be far behind.

One elegant equation was a nice dream — but with complexity creeping in, it’s time to switch tracks.

Time to go modular. Time to divide. Time to conquer.

And the first stop on this new track of conquest? Classification.

refresher: classification.

Until now, we’ve been living in the world of regression — where the goal is to predict the exact value we care about, given some input features… or, more formally, representations.

But beyond that lies another powerful paradigm — grouping.

Groups — whether you call them classes, categories, collections, or something else — help us reason about similar things as a whole. By abstracting away individual quirks, they shift our focus from fine-grained details to broader patterns. And, as long as it’s useful, grouping can repeat, forming hierarchies — rice → grain → food → … and so on.

In machine learning, this notion of grouping appears in two main forms — clustering and classification.

In clustering, we define similarity — as a function over input features that measures closeness. The model then uses this definition to group things that lie close together in that space.
For example, if we represent grains by their length and width, and define similarity as Euclidean distance, similar sized grains will be grouped together.
In classification, we demonstrate similarity — by providing labeled examples for the groups we care about. The model then uses these examples to learn a mapping from input features to those groups.
For example, if we label some grains as rice or wheat, the model will learn to assign those labels to new grains based on their length and width.

To prep ourselves for classification, we need to put on our supervisor hat — and that means creating labeled examples by tagging each data point with its grain type. The labels themselves can be anything really — white rice, brown rice, franken-grain — as long as they clearly separate our groups.

So let’s say we did just that — rolled up our sleeves, labeled our data, grouped the grains, and handed everything off to a classic: the softmax classifier.

This classifier looks at the grain’s darkness ( $z$ ) and outputs three probabilities — one for each grain type — indicating how likely it is to belong to each. For example, if $z$ is close to $0$ (a very light grain), it might give white rice a high probability ( $\approx 0.95$ ), with the remaining $0.05$ spread across the other two.

refresher: softmax classifier.

In machine learning, we often enter regression through linear regression — the simplest, most intuitive place to start. For classification, that starting point is logistic regression.

Like linear regression, logistic regression also starts by applying a linear function to the input… and it too regresses to a number. But in between, it applies the sigmoid function:

\sigma(z) = \frac{1}{1 + e^{-z}}

This squashes everything into the $0-1$ range — with large positives close to $1$ and large negatives close to $0$ . And yes, this is the same sigmoid you may remember as a classic activation function from Section 5.

Cool. So what the heck does this have to do with classification?

Well, if there are just two groups — an in group and an out group — our linear function can map input features to a number, or more formally, a score that is large for the in group and small, otherwise. Then, our sigmoid squashes this score into the $0-1$ range — which can now be interpreted as the probability of belonging to the in group.

Stepping back, this idea — using a function with a fixed set of parameters to map features to scores that reflect “group affinity” — is the essence of a parametric classifier. Logistic regression is one such classifier, and because the mapping function is linear, it’s also a linear classifier.

Like linear regression, we can use gradient descent to learn these parameters — but instead of getting a line that predicts exact values, we get a line that divides the input space into two groups.

Cool. But what if there are more than two groups?

We can simply extend the same idea with a linear function per group. Then,

if we stick to our sigmoid function, we get a multi-label classifier — where an input’s group membership is judged independently.
This means an input can belong to several groups at once — for example, with high probabilities for rice, and food, and vegan.
if we switch to the softmax function, we get a multi-class classifier — where an input’s group membership is judged relative to others.
This means an input typically belongs to one group — for example, with a high probability for rice, or wheat, or franken-grain.

This softmax function is simply a generalization of our sigmoid. Instead of a single probability, it produces a probability distribution over all groups.

\text{softmax}(z)_i = \frac{e^{z_i}}{\sum_{j=1}^n e^{z_j}} \quad \text{for } i \in \{1,\ldots,n\}

And classifiers that use this softmax function are commonly called softmax classifiers.

So, how do we use these probabilities to switch between the linear models we’ve already learned?

A natural instinct is to simply chain the classifier to them.

It mirrors how we think — our own chain of thought: “Oh, what’s this? Looks like white rice. Okay — two cups of water per cup of rice.” One decision leads to the next, and so on.

softmax classifer as a switch — softmax classifier as a switch

In fact, this kind of chaining — stitching together separate models with bits of handwritten code — is pretty common in practice. You’ll often see it built as a pipeline, with each stage handling a different part of the problem — just like a factory assembly line where each trained worker completes their part and sends it down the line.

In our case, that would mean stitching together a pipeline with simple if-else statements. But wait — we’ve been down that road before. We don’t want to hand-code anything — we want the model to learn it all on its own. So, how do we do that?

Since we ultimately want just one output, a good starting point is to simply add up all the outputs from our grain-cooking models. It’s like having a bunch of chefs in the kitchen — all shouting their recipes at the same time.

Now, all we need is a way to use the classifier’s probabilities to switch off the ones we don’t want — by setting their outputs to zero. It’s like putting the wrong chefs on mute.

combined expert models — combining expert models

And that brings us back to neural networks — and our old friend, ReLU.

ReLU is like a smart switch. When its input drops below zero, it automatically shuts off and stops any signal from passing through. This makes it the perfect mute button to silence the wrong chefs in our kitchen.

How exactly? Well, right before ReLU kicks in, each unit applies a linear function over its inputs. If we feed in the classifier’s probabilities and assign large negative weights to the wrong classes, that linear function will dip below zero — and ReLU will cut the signal before it reaches the final output.

This is easier to understand with an illustration so let’s break it down for white rice.

combined switch — ReLU switching on for white rice and off for the rest.

In the figure above, our linear function has four inputs — the original $x$ (cups of grain) and three probabilities from the classifier — with the following weights:

$2$ for $x$ (our white rice model),
$0$ for the white rice probability,
and $-100$ for the other two.

Now, if the classifier thinks the grain is white rice ( $p \approx 1$ ), the output is:

2x + 0 - 0 - 0 = 2x

That’s our white rice model, and ReLU passes it straight through.

But if the classifier leans toward any other type, the output becomes:

2x - 100

… which, for any reasonable value of $x$ , is negative — so ReLU turns it off, and that pathway contributes nothing to the final output.

Of course, we’re not assigning these weights by hand. The hope is that the model will learn something similar on its own — guided by data, and optimized by gradient descent.

And if it does, we’ve got ourselves a switch — not a hand-coded if-else, but a learned, data-driven switch.

Extending this to all grain types, the familiar sight of a neural network starts to emerge.

relu network — a classifier and a ReLU network.

Now you might be wondering why we took such a long and winding route only to get back to a neural network. I mean, we already trained one with $x$ and $z$ as inputs in Section 5 — so why go through all this trouble?

Well, the reason was to get a feel for something fundamental about our reality — that it’s compositional. Or, in less fancy terms, that the big, complex world we experience is made of simpler, repeatable structures, endlessly layered and intertwined — like an eternal box of Lego.

It is this aspect that layers within neural networks exploit as they reverse engineer the world they observe. Each layer gives them the capacity to not only shape the pieces they receive — the transforms — but also choose the pieces that matter — the controls.

In our grainy world, the classifier and the three regressors are these transforms — mapping grain color to probabilities, or cups of grain to cups of water. But once we wire them together with ReLU activations, they also gain the control they need to work together — acting only when they are truly needed.

Of course, all this transforming and controlling can be crammed into a single hidden layer — but that would demand far more units, and far more parameters to optimize. Instead, by layering the network, we mirror the underlying structure — letting each layer handle a smaller slice of the problem, and making the whole network far more efficient.

transforms & controls — a useful simplification.

The notion of transforms and controls is introduced here as a simple way to think about functions and their compositions.

In practice, neural networks don’t really care about the tidy structure we imagine for them. They simply follow the path of least resistance to minimize error — driven entirely by the data they observe and the loss function they optimize.

So, just because a network has two layers doesn’t mean it will neatly structure itself into a classifier and a bunch of regressors.

Efficiency, however, isn’t just about stacking layers — it’s also about what’s happening inside them. Our beloved ReLU may be a smart switch, but controlling it means feeding in all the classifier’s outputs — right or wrong. That might be fine with three grain types, but scale it to a hundred and the parameters start to quickly pile up.

Why? Because switches like ReLU are controlled by inhibitory signals — negative weighted inputs that work to offset the positives. In electronics, that’s like a diode that turns off only when an opposing voltage is strong enough to cancel other inputs. Even the name ReLU — Rectified Linear Unit — is a nod to this diode-like behavior.

But not every switch relies on inhibition. Some are more efficient — flipped not by an offset, but an external control… one that is of a higher-order. In fact, the device you’re reading this on has billions, or even trillions, of one such switch: the tiny but mighty transistor.

And just as ReLUs approximate diodes, attention mechanisms approximate transistors.

refresher: diodes & transistors.

In electronics, a diode is a semiconductor device that allows current to flow in only one direction. It’s made by doping one side of a silicon crystal as p-type (with positively charged holes) and the other as n-type (with negatively charged electrons). Where the two regions meet, they form a neutral zone called the depletion region, which acts as a barrier for the flow of current.

To overcome this barrier, the voltage across the diode must reach a point called the threshold or the forward potential. When it does, the diode conducts and current flows freely. Drop back below it, and the depletion region widens, cutting off the flow.

This simple behavior makes a diode act like a switch — a physical analog of our ReLU. And it’s also the same behavior that lets diodes be wired together to build logic gates, and with it, boolean logic — the foundation of modern computing.

But to build logic gates more compactly and efficiently, we turn to a more powerful semiconductor device, the transistor. Like a diode, a transistor is also made by doping different regions of a silicon crystal into different types. But instead of two layers, it has three — arranged as either n-p-n or p-n-p.

While the diode has a single barrier that only incoming currents can push through, the transistor has a middle layer that acts as the control. By applying different voltages to it, the transistor can pass, block, or even amplify the current — acting as a more versatile switch that makes logic gates smaller, and more efficient.

9. attention, please!

We’re here. The finale.

Take a deep breath, pat yourself on the back, and gently boop your nose.

It’s time for some attention.

After the mushy madness of franken-grain, the need for a data-driven switch was clear. While our trusty ReLU tried to step in, it simply lacked the higher-order goodness we craved. Then we met the humble transistor — and with it, hope.

To pass that hope on to our networks, we just need to take a closer look at what the softmax classifier is already giving us.

True to its name, soft-max boosts the right grain by maxing out its score. For most inputs, that means one output close to $1$ and the rest near $0$ . While it’s common to see them as probabilities, we can also see them as switches — $1$ for on, and $0$ for off — if we just multiply them with our regressors.

Here’s what that looks like.

And just like that, all those extra inhibitory signals from ReLUs are gone… leaving you with something simpler, and far more efficient.

Now, if this is starting to look eerily familiar, that’s because it is. It’s actually not that different from the higher-order polynomial we used in section 6

y = (pz + q)x + b

… but now, instead of a simple linear function, we have a more complex interaction through the softmax classifier

y = 2xc_{1} + 3xc_{2} + xc_{3}

where

c_i = \text{softmax}(p_i z + q_i)

And with this, we’ve sidestepped the need for a universal grain truth, and instead built local truths that connect efficiently — grain color → grain type → water-to-grain ratio.

Of course, we can’t tell our neural networks to organize this way — nor can we expect them to. What we can do is give them the tools, and hope our data can help them find their way.

Which finally brings us to the attention layer — a way to activate our units through an external function, much like a transistor.

In its simplest form, it looks like this:

… where $\odot$ denotes element-wise multiplication, also known as the Hadamard product.

Here, because softmax favors the few over the many, it selects, or more generally, mixes, signals that are most relevant to the task. That makes it feel like the network is paying attention to the experts that matter — like listening only to our white-rice chef when cooking white rice. And because those softmax probabilities now act as weights, they’re commonly called attention weights.

With this setup, we’ve also sidestepped the need for a separate classifier — and the set of hand-labeled examples it requires. Instead, we can now rely on the attention layer to group things as needed, building its own vocabulary — one that’s a probability distribution over hidden, or latent, categories.

And there we have it — attention in neural networks, built from scratch.

Now, let’s put it into practice and let gradient descent cook — starting with the network structure from above.

did the model learn what we hoped?

At a glance, it looks like we’ve got a good fit. But to check if the model actually learned what we hoped, we need to look at their parameters.

We’ll start with the attention layer:

\begin{aligned} s_1 &= \;\;\;0.0 * x - 10.0 * z + 3.9 \\ s_2 &= \;\;\;0.2 * x - \;\;0.0 * z - 0.1 \\ s_3 &= -0.8 * x + \;\;9.2 * z - 2.8 \end{aligned}

Here, $s_i$ represents scores before softmax — and because softmax exponentiates before normalizing, negatives get very small while positives dominate.

With that in mind, let’s look at what happens when our model sees different grains.

When $z \approx 0$ (white rice), we get:
$\begin{aligned} s_1 &= \;\;\;3.9 \\ s_2 &= \;\;\;0.2 * x - 0.1 \\ s_3 &= -0.8 * x - 2.8 \end{aligned}$
For small values of $x$ , this makes $s_1 \gg 0$ while $s_2$ and $s_3$ are near or below zero — giving us $c_1 \approx 1$ , $c_2 \approx 0$ , $c_3 \approx 0$ as attention weights.
When $z \approx 1$ (franken-grain), we get:
$\begin{aligned} s_1 &= -6.1 \\ s_2 &= \;\;\;0.2 * x - 0.1 \\ s_3 &= -0.8 * x + 6.4 \end{aligned}$
For small values of $x$ , this makes $s_3 \gg 0$ while $s_1$ and $s_2$ are near or below zero — giving us $c_1 \approx 0$ , $c_2 \approx 0$ , $c_3 \approx 1$ as attention weights.

So, while not perfect, the model has still figured out that grouping makes the task easier — and that $z$ drives most of that grouping. But we can also see that this split isn’t always neat — like when $z \approx 0.5$ for brown rice.

On the other side of the network, here are the linear units controlled by the attention weights.

\begin{aligned} r_1 &= 1.9 * x + 0 * z - 0.5 \\ r_2 &= 2.1 * x - 29.2 * z + 20.3 \\ r_3 &= 1.0 * x - 0 * z + 0 \end{aligned}

Again, not perfect, but close. The model has mostly learned to ignore $z$ and landed on something not far from our expectations — $y = 2x$ for white rice and $y = x$ for franken-grain.

Brown rice, though, is where things blur. Instead of learning $y = 3x$ , it has found another path — one that still fits the data, but not in the way we expected.

And that’s the reminder from earlier — just because we expect a network to learn things the way we imagine, doesn’t mean it will. After all, they are limited to the data they see — just tiny slivers of the reality that we observe… at least for now.

what's up with brown rice?

While we can only guess, here’s one way to read what’s happening.

For $z \approx 0.5$ (brown rice), we get:

\begin{aligned} s_1 &= - 1.1 \\ s_2 &= \;\;\;0.2 * x - 0.1 \\ s_3 &= -0.8 * x + 1.8 \end{aligned}

Let’s check them at the edges of our dataset.

At $x=1$ , $s_1 = -1.1$ , $s_2 = 0.1$ , and $s_3 = 1.0$ .
At $x=5$ , $s_1 = -1.1$ , $s_2 = 0.9$ , and $s_3 = -2.2$ .

So for small $x$ , the attention weights favor franken-grain, and only shift toward brown rice as $x$ increases.

On the regressor side, at $z \approx 0.5$ we get

\begin{aligned} r_2 &= 2.1 * x - 5.7 \\ \end{aligned}

This looks similar to the white rice regressor, but with a large negative offset.

So why might this happen?

In our dataset, all expected regressors pass through the origin — since zero cups of grain means zero cups of water. For small $x$ , that means the observed differences in water needs are quite small. While they do get larger as $x$ grows, our toy dataset doesn’t really get that far.

So the model takes the easy way out. It settles on a weird blend of two regressors instead of separating them cleanly, and minimizes the loss without learning the pattern we expected.

model caveats.

Training these models can be finicky, especially with a toy dataset. So, to keep the narrative focused, this model was chosen from a small batch of runs (~10) to possess both low error and easily interpretable parameters.

Also, for readability, all parameters were rounded to one decimal place.

To really bring out the contrast with ReLU, let’s briefly leave our grain world behind for a similar but more general dataset — five linear relationships, each with a random slope and intercept, plus another variable that decides which one is active.

To model this, we’ll train an attention network like the one before — now with a size of $5$ ( $30$ parameters). For comparison, we’ll train two fully connected ReLU networks with similar parameter counts — one with a single hidden layer of size $7$ ( $29$ parameters), and another with two hidden layers of sizes $4$ and $3$ ( $31$ parameters).

As you can see, all three models fit the samples pretty well, but only the attention network does so in line with the underlying relationship. That’s because the linear units that model them — the values — stay as-is, leaving the attention layer to provide the keys to unlock the right ones.

In other words, there is a clearer separation of roles within our model architecture — an inductive bias — which makes for a more faithful model. And since the ReLU networks lack this, they fit the data in fragments, diffusing information across the network and missing the deeper patterns.

Of course, this is a toy example where everything is neat and tidy, but it shows the power of an external control — where expert selection is separated from their inner workings.

With deez nuts and bolts in place, here’s a fancy math version of our attention mechanism:

y = \sum_{i=1}^{n} f(u)_i \cdot \text{softmax}(g(v))_i

Until now, both $f(u)$ and $g(v)$ have been linear layers to keep things intuitive, but in general they can be any function. We could swap them out for a fully connected network, a convolutional network, or even another attention network — as long as both produce vectors of the same size.

To get a feel for this, imagine that we replaced the variable $z$ (grain darkness) with photos of the grains we cooked. Now, with $z$ as a bunch of pixels, we can use a convolutional neural network as our $g(v)$ , and plug the result into our attention layer like before.

Since we have two networks, each with its own inputs, and the output of one crosses over to act as weights for the other, this setup is called cross-attention. In fact, the term attention first appeared on the horizon in this context, where signals from an encoder network were used as weights for a decoder network.

The more common variant, though, is self-attention, best known from the ubiquitous transformer architecture. Here, as the name suggests, the same inputs flow to both sides, though the functions that transform them are far more complex.

But that complexity marks the start of another journey, one that is already mapped out by many other posts. So for us, the grain train has reached its final stop.

Beyond this station, the tracks spread into a forest of attention mechanisms, each branching into a different corner of the AI landscape. Yet in spirit, they remain close to our grainy intuition — higher-order networks that learn how to mix expert signals, and weave narrow views into broader understanding.

… and that’s a wrap!

If you’ve made it this far, you’ve earned yourself a big bag of cheetos, a tall glass of coke, and of course, a giant tub of ice cream.

I hope this post helped your intuition, and becomes a bridge to learn more.

And on that note, here’s a quick shout out to the people who were my bridges to this post.

I first came across the attention ↔ transistor analogy a few years ago in NYU’s Deep Learning Course taught by Yann LeCun & Alfredo Canziani. I loved it so much that it became the singular source of inspiration & insight for this post.
Also, thanks to Eli Bressert, Abhinav Sharma and Claudia Vanea for being early sounding boards and reviewers.

If you liked this post and want to hear about new ones, drop your email below.

Attention in Neural Networks from Scratch